
Ministério da Saúde adverte: Ler esse post e assistir Inception pode tostar o seu cérebro! Sim amigo , outro post gigante de “fundir a cuca”. Podemos prever: 30 % das pessoas irão ler apenas o título e fugirão para as colinas, 20% vai ler a primeira frase e reclamar: “Ah, é muito grande!Mimimi!”, 10% terão preguiça até mesmo de clicar para abrir o post, 10% irão ler até a metade, 10% irão ler da metade em diante,5% perceberão que nem o autor do tópico compreende por completo todas essas maluquices, 5% irão ler tudo e não entender a metade, 9% irão ler a metade e entender tudo, 0,5% irão ler tudo e entender tudo, 0,5% ficarão loucas e saíram se debatendo nuas pela cidade onde vivem, 20% já pararam de ler no “30% das pessoas…”, 40% já perceberão que essa estatística é uma furada. 200,01% dos que chegarão até aqui clicaram de imediato no
10. Realidade simulada


Realidade simulada é a proposição de que a realidade poderia ser simulada – talvez por modelagem computacional – a uma qualidade indistinguível da realidade “verdadeira”. Ela poderia conter mentes conscientes que poderiam ou não saber que estão vivendo dentro de uma simulação. Na sua forma mais intensa, a “hipótese da simulação” (simulation hypothesis) ou “simulismo” (simulism) alega que é provável que estejamos vivendo tal simulação.
É diferente do conceito corrente e tecnologicamente atingível de realidade virtual. Realidade virtual é facilmente distinguível da experiência da realidade “verdadeira” – participantes nunca tem dúvida sobre em qual realidade estão. Em contraste, seria difícil ou mesmo impossível definir quando se está dentro de uma realidade simulada.
A idéia de realidade simulada levanta uma série de questões:
É diferente do conceito corrente e tecnologicamente atingível de realidade virtual. Realidade virtual é facilmente distinguível da experiência da realidade “verdadeira” – participantes nunca tem dúvida sobre em qual realidade estão. Em contraste, seria difícil ou mesmo impossível definir quando se está dentro de uma realidade simulada.
A idéia de realidade simulada levanta uma série de questões:
É possível, mesmo em princípio, dizer se estamos ou não em uma realidade simulada?
Há alguma diferença entre uma realidade simulada e uma “realidade real”?
Como deveríamos nos comportar se descobríssemos que estamos dentro de uma simulação?
Os cientistas que estudam essa possibilidade afirmam que coisas simples da vida, como um dejà-vu por exemplo, poderiam ser sinais de uma provável realidade simulada existente. Apesar de não haver prova concreta, acredita-se que sensações como o dejà-vu seriam falhas no sistema que controla essa situação de simulismo, permitindo que as mentes tivessem plena consciência de fatos antes de seu ocorrido. Deve se levar em conta a percepção humana de que o tempo “corre para frente”, ou seja, o dejá-vu seria fisicamente impossível, já que não há como ter uma sensação de já ter visto algo, se ainda não aconteceu. As falhas desse sistema nos permite portanto antever situações que ainda não ocorreram, já que são apenas simulação e já estão pré-programadas dentro da mente inconsciente. Esses exemplos entre outros provariam que o que entendemos por realidade possa de alguma forma estar co-relacionada a idéia de simulismo. Entretanto, vê-se num paradigma, já que a mente humana, apesar de inconsciente, já conseguiu chegar a esse tipo de conclusão sobre o sistema que, hipoteticamente, nos manteria inconscientes. Seria-mos portanto conscientes de nossa inconsciência, o que é algo a se pensar nesse sentido.
9. Teorema do Macaco Infinito


O Teorema do macaco infinito afirma que um macaco digitando aleatoriamente em um teclado por um infinito espaço de tempo irá quase certamente criar um texto qualquer escolhido, como por exemplo a obra completa de William Shakespeare.
Pode-se também pensar que, com infinitos macacos infinitos, algum deles irá quase certamente criar um texto qualquer escolhido como primeiro texto a ser digitado.
Neste contexto, “quase certamente” é um termo matemático com um significado preciso, enquanto que o “macaco” é apenas uma imagem, não um símio verdadeiro; trata-se de uma metáfora para um dispositivo abstracto que produza uma sequência aleatória de letras ad infinitum. O teorema ilustra os perigos do raciocínio sobre o infinito ao imaginar um número muito grande mas finito, e vice versa. A idade do universo é diminuída relativamente pelo tempo que levaria a um macaco para obter um texto igual ao Hamlet, de modo que num sentido físico tal nunca aconteceria.
Variantes do teorema incluem múltiplos dispositivos de escrita, e o texto pode variar entre uma biblioteca inteira e uma simples e pequena frase. A história deste tipo de afirmações remonta à Metafísica de Aristóteles e ao De natura deorum de Cícero, passa por Blaise Pascal e Jonathan Swift, e finalmente às afirmações recentes com os icónicos escritores infinitos. No início do século XX, Émile Borel e Arthur Eddington usaram o teorema para ilustrar as escalas temporais implícitas nos fundamentos da mecânica estatística. Vários apologetas cristãos por um lado, e Richard Dawkins por outro, argumentaram sobre a adequação de macacos como metáfora para a evolução.
Pode-se também pensar que, com infinitos macacos infinitos, algum deles irá quase certamente criar um texto qualquer escolhido como primeiro texto a ser digitado.
Neste contexto, “quase certamente” é um termo matemático com um significado preciso, enquanto que o “macaco” é apenas uma imagem, não um símio verdadeiro; trata-se de uma metáfora para um dispositivo abstracto que produza uma sequência aleatória de letras ad infinitum. O teorema ilustra os perigos do raciocínio sobre o infinito ao imaginar um número muito grande mas finito, e vice versa. A idade do universo é diminuída relativamente pelo tempo que levaria a um macaco para obter um texto igual ao Hamlet, de modo que num sentido físico tal nunca aconteceria.
Variantes do teorema incluem múltiplos dispositivos de escrita, e o texto pode variar entre uma biblioteca inteira e uma simples e pequena frase. A história deste tipo de afirmações remonta à Metafísica de Aristóteles e ao De natura deorum de Cícero, passa por Blaise Pascal e Jonathan Swift, e finalmente às afirmações recentes com os icónicos escritores infinitos. No início do século XX, Émile Borel e Arthur Eddington usaram o teorema para ilustrar as escalas temporais implícitas nos fundamentos da mecânica estatística. Vários apologetas cristãos por um lado, e Richard Dawkins por outro, argumentaram sobre a adequação de macacos como metáfora para a evolução.
8. A Experiência da Gravidade
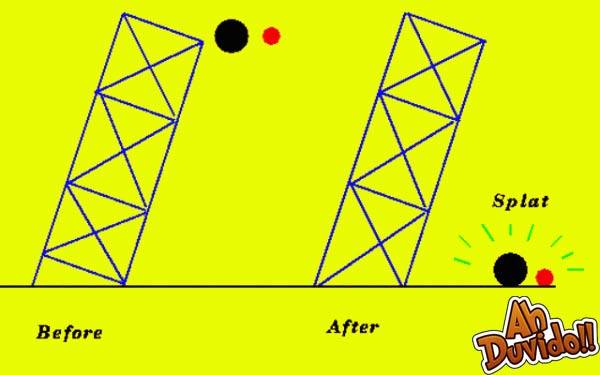

Ao contrário do que os professores costumam dizer, Galileu Galilei provavelmente não soltou bolas da Torre de Pisa, ou qualquer outro objeto. A experiência da gravidade foi realizada no laboratório da sua mente. Seus colegas do século 16 acreditavam que os objetos pesados cairiam mais rapidamente que os leves. Assim, Galileu imaginou uma bola pesada presa por uma corda com uma bola leve. De acordo com a lógica aristotélica, se o objeto de luz e o objeto pesado fossem amarrados e caíssem de uma torre, o objeto mais pesado cairia mais rápido, e a corda entre os dois sofreria uma tensão . Isso permitiria que o objeto mais leve atrasasse a queda do mais pesado, visto que este teria que “arrasta-lo” para baixo. Assim Galileu argumentou que uma vez que isso ocorre, o peso dos dois objetos deveria ser maior que o peso deles separadamente. Então concluiu que eles atingiriam o solo simultaneamente.
7. O Problema da Parada


Na teoria da computabilidade, o problema da parada é um problema de decisão que pode ser formulado da seguinte forma: Dado uma descrição de um programa e uma entrada finita, decida se o programa termina de rodar ou rodará indefinidamente, dada essa entrada.. Isso é equivalente ao problema de decidir, tendo em conta um programa e uma entrada, se o programa irá eventualmente parar quando executado com essa entrada, ou vai rodar para sempre. Alan Turing provou em 1936 que um algoritmo genérico para resolver o problema da parada para todos pares programa-entrada possíveis não pode existir. Dizemos que o problema da parada é indecidível nas Máquinas de Turing.
A importância histórica do problema da parada reside no fato de que foi um dos primeiros problemas a ser provado indecidível. (A prova de Turing foi lançada em maio de 1936, enquanto a prova de Alonzo Church da indecidibilidade de um problema no cálculo lambda já havia sido lançada em abril de 1936). Subsequentemente, muitos outros problemas foram descritos; o método típico de provar que um problema é indecidível é a técnica de redução. Para isso, o cientista da computação mostra que se uma solução para o novo problema foi encontrada, ela poderia ser usada para decidir um problema indecidível (transformando instâncias do problema indecidível em instâncias do novo problema). Como sabemos de antemão que nenhum método pode decidir o problema antigo, então nenhum método pode decidir o problema novo também.
Uma consequência da indecidibilidade do problema da parada é que não pode existir um algoritmo genérico que decida se um dado enunciado sobre os números naturais é verdadeiro ou falso. A razão para isso é que a proposição que afirma que um certo algoritmo vai parar dado uma certa entrada pode ser convertido em um enunciado equivalente sobre os números naturais. Se nós tivéssemos um algoritmo que pudesse resolver todo enunciado sobre os números naturais, ele certamente poderia resolver tal enunciado; mas isso determinaria se o problema original para o que é impossível, já que o problema da parada é indecidível.
Outra consequência da indecidibilidade do problema da parada é o Teorema de Rice que enuncia que a verdade de qualquer enunciado não-trivial sobre a função definida por um algoritmo é indecidível. Então, por exemplo, o problema da parada “esse algoritmo parará para a entrada 0″ já é indecidível. Perceba que esse teorema considera a função definida pelo algoritmo e não o algoritmo propriamente dito. É, por exemplo, possível decidir se um algoritmo vai parar dentro de 100 passos, mas isso não é um enunciado sobre a função que é definida pelo algoritmo.
Gregory Chaitin definiu uma probabilidade de parada, representada pelo símbolo ?, um tipo de número real que informalmente representa a probabilidade que um programa produzido aleatoriamente pare. Esses números têm o mesmo grau de insolubilidade da Teoria da Computação e da Complexidade Computacional que o problema da parada. É um número normal e um número transcendenteque pode ser definido mas não completamente computado. Isso significa que pode ser provado que não existe algoritmo que produza dígitos de ?, embora seja possível calcular seus primeiros dígitos nos casos simples.
Enquanto a prova de Turing mostrou que não pode existir algoritmo ou método genérico para determinar se um algoritmo para, instâncias individuais de um problema podem muito bem ser suscetíveis a ataques. Dado um algoritmo específico, um pode geralmente mostrar que ele deve parar para qualquer entrada, e de fato cientistas da computação geralmente fazem isso como parte de uma prova exata. Mas cada prova tem que ser desenvolvida especificamente para o algoritmo em mãos; não existe modo mecânico ou genérico para determinar se algoritmos em Máquinas de Turing param. Entretanto, existem algumas heurísticas que podem ser usadas para tentar-se construir uma prova, que freqüentemente dão seguimento a programas típicos.
A introdução de Turing do modelo de máquina que posteriormente ficou conhecido como Máquinas de Turing, introduzido no artigo, provou-se um modelo muito conveniente para a Teoria da Computação.
A importância histórica do problema da parada reside no fato de que foi um dos primeiros problemas a ser provado indecidível. (A prova de Turing foi lançada em maio de 1936, enquanto a prova de Alonzo Church da indecidibilidade de um problema no cálculo lambda já havia sido lançada em abril de 1936). Subsequentemente, muitos outros problemas foram descritos; o método típico de provar que um problema é indecidível é a técnica de redução. Para isso, o cientista da computação mostra que se uma solução para o novo problema foi encontrada, ela poderia ser usada para decidir um problema indecidível (transformando instâncias do problema indecidível em instâncias do novo problema). Como sabemos de antemão que nenhum método pode decidir o problema antigo, então nenhum método pode decidir o problema novo também.
Uma consequência da indecidibilidade do problema da parada é que não pode existir um algoritmo genérico que decida se um dado enunciado sobre os números naturais é verdadeiro ou falso. A razão para isso é que a proposição que afirma que um certo algoritmo vai parar dado uma certa entrada pode ser convertido em um enunciado equivalente sobre os números naturais. Se nós tivéssemos um algoritmo que pudesse resolver todo enunciado sobre os números naturais, ele certamente poderia resolver tal enunciado; mas isso determinaria se o problema original para o que é impossível, já que o problema da parada é indecidível.
Outra consequência da indecidibilidade do problema da parada é o Teorema de Rice que enuncia que a verdade de qualquer enunciado não-trivial sobre a função definida por um algoritmo é indecidível. Então, por exemplo, o problema da parada “esse algoritmo parará para a entrada 0″ já é indecidível. Perceba que esse teorema considera a função definida pelo algoritmo e não o algoritmo propriamente dito. É, por exemplo, possível decidir se um algoritmo vai parar dentro de 100 passos, mas isso não é um enunciado sobre a função que é definida pelo algoritmo.
Gregory Chaitin definiu uma probabilidade de parada, representada pelo símbolo ?, um tipo de número real que informalmente representa a probabilidade que um programa produzido aleatoriamente pare. Esses números têm o mesmo grau de insolubilidade da Teoria da Computação e da Complexidade Computacional que o problema da parada. É um número normal e um número transcendenteque pode ser definido mas não completamente computado. Isso significa que pode ser provado que não existe algoritmo que produza dígitos de ?, embora seja possível calcular seus primeiros dígitos nos casos simples.
Enquanto a prova de Turing mostrou que não pode existir algoritmo ou método genérico para determinar se um algoritmo para, instâncias individuais de um problema podem muito bem ser suscetíveis a ataques. Dado um algoritmo específico, um pode geralmente mostrar que ele deve parar para qualquer entrada, e de fato cientistas da computação geralmente fazem isso como parte de uma prova exata. Mas cada prova tem que ser desenvolvida especificamente para o algoritmo em mãos; não existe modo mecânico ou genérico para determinar se algoritmos em Máquinas de Turing param. Entretanto, existem algumas heurísticas que podem ser usadas para tentar-se construir uma prova, que freqüentemente dão seguimento a programas típicos.
A introdução de Turing do modelo de máquina que posteriormente ficou conhecido como Máquinas de Turing, introduzido no artigo, provou-se um modelo muito conveniente para a Teoria da Computação.
6. O Argumento do Dia do Juízo Universal


O argumento do Dia do Juízo Universal foi concebido pelo astrofísico Brandon Carter há uns quinze anos e foi, desde então, desenvolvido em um artigo da “Nature” por Richard Gott (1993) e em vários documentos, pelo filósofo John Leslie, especialmente em sua recente monografia, “O Fim do Mundo” (Leslie, 1996). A idéia principal é esta: imagine que duas urnas grandes são postas na sua frente; e você sabe que uma delas contém dez bolas e a outra um milhão, mas você não sabe distinguí-las. Você sabe que as bolas em cada urna são numeradas em 1, 2, 3,… N. Agora você sorteia uma bola ao acaso da urna esquerda, que é a de número 7. Claramente este é um forte indício de que aquela urna contém só dez bolas. Se originalmente as chances fossem cinqüenta em cinqüenta, uma aplicação rápida do teorema de Bayes lhe daria a probabilidade posterior de que a urna esquerda é a que contém somente dez bolas. (Pposterior (L=10)=0.999990). Mas agora considere um caso onde em vez de urnas você tem duas possíveis gerações de humanos e em vez de bolas você tem indivíduos enfileirados de acordo com a origem. De fato você vem a achar que sua posição na fila é aproximadamente de sessenta bilhões. Agora, dizem Carter e Leslie, nós devemos raciocinar do mesmo modo como fizemos com as urnas. Para que você deva ter uma posição entre sessenta bilhões, ou aproximadamente isso, é muito mais provável se apenas 100 bilhões de pessoas já terão vivido do que se existirão muitos trilhões de pessoas. Portanto, através do teorema de Bayes, você deve atualizar suas convicções sobre os prospectos do gênero humano e perceber que um Dia do Juízo Universal iminente é muito mais provável do que você tem pensado até agora.
Considere a objeção: “Mas a probabilidade de eu ter qualquer determinada posição não é sempre mais baixa conforme quanto mais pessoas terão existido? Eu devo ser raro em alguns detalhes e qualquer posição em particular seria altamente improvável; mas seguramente este não pode ser usado como um argumento para mostrar que existem provavelmente somente algumas pessoas?”.
Para que uma mudança de probabilidade ocorra, você tem de pôr em evidência o que é mais provável em uma hipótese do que na outra. Quando você considera sua posição no Argumento do Dia do Juízo Universal, o único fato relevante sobre este valor é que ele é mais baixo do que o número total de indivíduos que teriam existido em qualquer uma das hipóteses, mas, apesar de te tudo que você sabia, poderia ter sido um número mais alto do que o número total de pessoas que teriam vivido em uma das hipóteses, assim, refutando aquela hipótese. Não faz diferença se você executar o cálculo com uma posição específica ou um intervalo dentro do qual a posição verdadeira se encontra. O cálculo Bayesiano produz a mesma probabilidade posterior. O fato de você descobrir que tem esta posição particular só lhe dá informação porque você não sabia que não descobriria um valor de posição, que teria sido incompatível com a hipótese de que teriam existido somente alguns indivíduos. Pressupõe-se que você sabia quais valores de posição eram compatíveis com quais hipóteses. É verdade que para qualquer valor de posição em particular, achar que você tem aquele valor de posição é um evento improvável, mas uma mudança de probabilidade não acontece por causa de sua própria improbabilidade, mas por causa da diferença entre suas probabilidades condicionais relativas às duas hipóteses.
Há numerosas objeções como esta aqui que podem ser facilmente vistas como equívocos. A maioria das pessoas quando se confronta com este argumento está pouco disposta a aceitá-lo. Há algo intuitivamente perverso sobre isto. Porém quando se trata de fazer das intuições explícitas e explicar exatamente por que o argumento se torna inadequado, não há qualquer sinal de consenso: cada um tem a sua própria teoria sobre o que saiu errado. Eu acho que muitas supostas refutações foram com sucesso anuladas por Leslie, e aqueles que acreditam que podem compreender imediatamente por que o argumento esboçado acima não dá certo, podem achar que vale a pena dar uma olhada nos capítulos 5 e 6, do livro de Leslie.
Se o argumento do Dia do Juízo Universal falha ou não em dar qualquer predição válida sobre o futuro, seu status é ainda controverso, e é claramente em parte um problema filosófico determinar a sua eventual validade (e em parte um problema de teoria das probabilidades).
Considere a objeção: “Mas a probabilidade de eu ter qualquer determinada posição não é sempre mais baixa conforme quanto mais pessoas terão existido? Eu devo ser raro em alguns detalhes e qualquer posição em particular seria altamente improvável; mas seguramente este não pode ser usado como um argumento para mostrar que existem provavelmente somente algumas pessoas?”.
Para que uma mudança de probabilidade ocorra, você tem de pôr em evidência o que é mais provável em uma hipótese do que na outra. Quando você considera sua posição no Argumento do Dia do Juízo Universal, o único fato relevante sobre este valor é que ele é mais baixo do que o número total de indivíduos que teriam existido em qualquer uma das hipóteses, mas, apesar de te tudo que você sabia, poderia ter sido um número mais alto do que o número total de pessoas que teriam vivido em uma das hipóteses, assim, refutando aquela hipótese. Não faz diferença se você executar o cálculo com uma posição específica ou um intervalo dentro do qual a posição verdadeira se encontra. O cálculo Bayesiano produz a mesma probabilidade posterior. O fato de você descobrir que tem esta posição particular só lhe dá informação porque você não sabia que não descobriria um valor de posição, que teria sido incompatível com a hipótese de que teriam existido somente alguns indivíduos. Pressupõe-se que você sabia quais valores de posição eram compatíveis com quais hipóteses. É verdade que para qualquer valor de posição em particular, achar que você tem aquele valor de posição é um evento improvável, mas uma mudança de probabilidade não acontece por causa de sua própria improbabilidade, mas por causa da diferença entre suas probabilidades condicionais relativas às duas hipóteses.
Há numerosas objeções como esta aqui que podem ser facilmente vistas como equívocos. A maioria das pessoas quando se confronta com este argumento está pouco disposta a aceitá-lo. Há algo intuitivamente perverso sobre isto. Porém quando se trata de fazer das intuições explícitas e explicar exatamente por que o argumento se torna inadequado, não há qualquer sinal de consenso: cada um tem a sua própria teoria sobre o que saiu errado. Eu acho que muitas supostas refutações foram com sucesso anuladas por Leslie, e aqueles que acreditam que podem compreender imediatamente por que o argumento esboçado acima não dá certo, podem achar que vale a pena dar uma olhada nos capítulos 5 e 6, do livro de Leslie.
Se o argumento do Dia do Juízo Universal falha ou não em dar qualquer predição válida sobre o futuro, seu status é ainda controverso, e é claramente em parte um problema filosófico determinar a sua eventual validade (e em parte um problema de teoria das probabilidades).
5. Cérebro numa cuba


Um dos experimento mentais mais influente, o ” cérebro numa cuba”é uma hipótese que permeou tudo, desde a ciência cognitiva até filosofia da cultura popular. O experimento pede-lhe para imaginar um cientista louco que tomou o seu cérebro de seu corpo e colocou-o em uma cuba de algum tipo de fluido de sustentação da vida. Eletrodos foram conectados ao seu cérebro, e estes são conectados a um computador que gera imagens e sensações. Uma vez que todas as informações sobre o mundo é filtrada através do cérebro, este computador teria a capacidade de simular a sua experiência cotidiana. Se isso fosse realmente possível, como você pôde verdadeiramente provar que o mundo à sua volta era real, e não apenas uma simulação gerada por um computador? Se você está pensando que tudo isso soa um pouco como The Matrix , você está certo.
4. Paradoxo de Ross-Littlewood


O problema do pote e das bolinhas, conhecido no meio técnico como o Paradoxo de Ross-Littlewood, é um exercício mental (id est algo impossível de se fazer na prática) que serve para exemplificar a natureza contraintuitiva do infinito.
A ideia é a seguinte: suponha que você tenha um pote infinitamente grande (não, não é o mesmo que você usa para guardar biscoitos) e uma pilha infinita de bolinhas. O exemplo clássico é que elas sejam de pingue-pongue, o que justifica o outro nome que o problema pode levar – ping pong ball problem. Para todos os efeitos, não importa a bolinha. O que você vai fazer com elas é o seguinte:
Numere bolinhas de 1 a 10 e coloque todas no pote. Retire a de número 1. Depois, numere bolinhas de 11 a 20, adicione-as ao pote e retire a de número 2. Seguindo o mesmo padrão, numere bolinhas de 21 a 30 e retire a de número 3. Continue o processo indefinidamente, sempre observando a mesma lógica e sem nunca parar. Não reclame: você tem infinitas bolinhas!
Isso pode levar algum tempo. Mas, para nosso problema resultar num paradoxo, você também deve estar de olho no relógio. O processo todo deve ser iniciado precisamente às 11 horas, 59 minutos e 30 segundos de um dia qualquer. Escolha um dia em que você não esteja com muita pressa para o almoço. O primeiro passo deve ser feito em 15 segundos. O segundo, em 7 segundos e meio. O terceiro, na metade disso e assim por diante, de forma que, ao meio-dia, você tenha executado um número infinito de passos.
Parece confuso? Você ainda não viu nada. Se não entendeu o espírito, peço que siga de novo o raciocínio dos passos, dessa vez com a nossa restrição cronológica:
Comece às 11 horas, 59 minutos e 30 segundos. Numere bolinhas de 1 a 10 e adicione-as ao pote. Retire a de número 1. Esse processo deve demorar 15 segundos. Agora, numere bolinhas de 11 a 20, adicione-as ao pote e retire a de número 2. Esse passo deve demorar a metade do tempo do primeiro, ou seja, 7 segundos e meio. Para continuar, numere bolinhas de 21 a 30 e retire a de número 3, cuidando para que o tempo desse passo seja metade do segundo. Continue repetindo a operação infinitamente, sempre adicionando dez bolinhas, retirando a de menor número e fazendo este processo na metade do tempo que você levou para fazer o anterior.
A grande questão paradoxal é: QUANTAS BOLINHAS HAVERÁ NO POTE AO MEIO-DIA?
Pare, pense e tente conviver (um pouco) com essa dúvida antes de ler a resposta.
A grande questão paradoxal é: QUANTAS BOLINHAS HAVERÁ NO POTE AO MEIO-DIA?
Pare, pense e tente conviver (um pouco) com essa dúvida antes de ler a resposta.
As soluções
A maioria das pessoas pensa de imediato em uma das duas alternativas: 1) o pote está infinitamente cheio, pois se adiciona mais bolas do que se retira; ou 2) o meio-dia nunca chegará. As duas respostas podem ser válidas, mas no caso desse paradoxo, ainda há mais alternativas a serem consideradas!
Por increça que parível o pote, ao final de todo esse tira-põe e deixa-ficar de bolinhas, pode estar infinitamente cheio ou infinitamente vazio!
Como isto é possível? Matemágica?
Não. Pura e simples lógica. Esse é o problema de se brincar com quantidades infinitas. Acompanhem:
1) O pote está infinitamente cheio
O campeão de chutes é justamente esse. Eu diria que, pessoalmente, logo de cara, é o pensamento mais sedutor. Afinal, tira-se uma bolinha e adiciona-se outras dez, de forma que o saldo final sempre fica positivo em mais nove bolinhas. Assim, a cada passo N, teríamos 9N bolinhas dentro do pote, o que é perfeitamente lógico.
2) O pote está vazio
A primeira vista, esta solução é de torcer os neurônios, mas, após uma pequenina análise, é tão lógico quanto assumir que o pote está infinitamente cheio.
Pense, por exemplo, na bolinha de número 4001. Ela foi adicionada no passo de número 400, da mesma forma que a número 21 foi adicionada no passo 2 e a 51 no passo 5. Contudo, no passo de número 4001, a bola 4001 foi retirada! E, tendo em vista que temos infinitos passos antes do meio-dia, sempre que pensarmos em QUALQUER bola numerada podemos ditar o passo no qual ela foi retirada.
Sendo assim, o pote está vazio ao meio-dia.
Pense, por exemplo, na bolinha de número 4001. Ela foi adicionada no passo de número 400, da mesma forma que a número 21 foi adicionada no passo 2 e a 51 no passo 5. Contudo, no passo de número 4001, a bola 4001 foi retirada! E, tendo em vista que temos infinitos passos antes do meio-dia, sempre que pensarmos em QUALQUER bola numerada podemos ditar o passo no qual ela foi retirada.
Sendo assim, o pote está vazio ao meio-dia.
Surpreso? Esse é o problema de exercícios mentais com a escorregadia palavra de quatro sílabas: infinito. Há ainda pessoas que apontam problemas estruturais no enunciado do paradoxo; há quem faça menção ao Paradoxo de Zenão (o caso do meio-dia que nunca chega); preferi deixar de lado essas opções e, para quem queira pesquisar.
3. O Demônio de Maxwell


De acordo com a segunda lei da termodinâmica, a entropia de um sistema isolado não diminui (Todo Sistema abandonado à sua própria sorte se degenera). Para mostrar que tal lei tem caráter estatístico, J.C. Maxwell, nos idos de 1871, argumentou que a presença de um demônio inteligente microscópico violaria essa lei!
Esse minúsculo ser inteligente conseguiria observar o estado microscópico de um sistema físico e aproveitar a ocorrência de flutuações favoráveis para diminuir a entropia.
Segundo Maxwell:
Esse minúsculo ser inteligente conseguiria observar o estado microscópico de um sistema físico e aproveitar a ocorrência de flutuações favoráveis para diminuir a entropia.
Segundo Maxwell:
“Mas se concebermos um ser cujas faculdades são tão aguçadas que ele consegue acompanhar cada molécula em seu curso, tal ser, cujos atributos são ainda essencialmente tão finitos quantos os nossos, seria capaz de fazer o que atualmente nos é impossível fazer. Pois vimos que as moléculas em um recipiente cheio de ar a uma temperatura uniforme movem-se com velocidades que não são de modo algum uniformes. Suponhamos agora que tal recipiente é separado em duas porções, A e B, por meio de uma divisória no qual há um pequeno orifício, e que um ser, que pode ver as moléculas individuais, abre e fecha este orifício, de forma a permitir que somente as moléculas mais rápidas passem de A para B, e somente as mais lentas passem de B para A. Ele irá portanto, sem gasto de trabalho, elevar a temperatura de B e abaixar a de A, em contradição à 2ª lei da termodinâmica.”
Por que este demônio não viola a 2ª lei da termodinâmica?
Desde então, inúmeros físicos tentaram escapar desta possibilidade. Szilard (1929) fez um grande avanço ao argumentar que a queda de entropia do gás seria compensada por um aumento de entropia na cabeça do demônio. Esmiuçando esta idéia, na década de 50, Brillouin e Gabor argumentaram que é a medição que o demônio faz da posição de uma molécula que levaria a um aumento compensatório de entropia (a absorção de um fóton dissipa energia).
Quando tudo parecia resolvido, Charles H. Bennett – que ficara famoso por ter mostrado que é possível fazer qualquer computação de maneira reversível – mostrou que é o apagamento de informação que dissipa energia no demônio, e não a mera realização de uma medição!
Esta explicação é hoje hegemônica, mas ainda há discípulos de Brillouin que a combatem! Quem terá razão?
Desde então, inúmeros físicos tentaram escapar desta possibilidade. Szilard (1929) fez um grande avanço ao argumentar que a queda de entropia do gás seria compensada por um aumento de entropia na cabeça do demônio. Esmiuçando esta idéia, na década de 50, Brillouin e Gabor argumentaram que é a medição que o demônio faz da posição de uma molécula que levaria a um aumento compensatório de entropia (a absorção de um fóton dissipa energia).
Quando tudo parecia resolvido, Charles H. Bennett – que ficara famoso por ter mostrado que é possível fazer qualquer computação de maneira reversível – mostrou que é o apagamento de informação que dissipa energia no demônio, e não a mera realização de uma medição!
Esta explicação é hoje hegemônica, mas ainda há discípulos de Brillouin que a combatem! Quem terá razão?
2. Gato de Schrodinger


O Gato de Schrödinger é um experimento mental, freqüentemente descrito como um paradoxo, desenvolvido pelo físico austríaco Erwin Schrödinger em 1935. Isso ilustra o que ele observou como o problema da interpretação de Copenhague da mecânica quântica sendo aplicado a objetos do dia-a-dia, no exemplo de um gato que pode estar vivo ou morto, dependendo de um evento aleatório precedente. No curso desse experimento, ele criou o termo Verschränkung
Sobre o experimento, Schrödinger escreveu:
“Qualquer um pode mesmo montar casos bem ridículos. Um gato é preso em uma câmara de aço, enquanto com o dispositivo seguinte (o qual deve estar seguro contra interferência direta do gato): em um contador Geiger tem uma pequena quantidade de substância radioativa, tão pequena, que talvez durante o período de uma hora, um dos átomos decaia, mas também, com a mesma probabilidade, talvez nenhum; se isso acontecer, o tubo do contador descarrega e através de um relé libera um martelo que quebra um pequeno frasco de ácido cianídrico. Se algum deles tiver saído do seu sistema natural por uma hora, alguém pode concluir que o gato permanece vivo enquanto o átomo não tiver decaído. Afunção-psi do sistema poderia ser expresso por ter dentro dele o gato morto-vivo (com o perdão da palavra) misturada ou dividido em partes iguais.
É típico desses casos que uma indeterminação originalmente restrita ao domínio atômico tenha sido transformada em uma indeterminação macroscópica, o qual pode então ser resolvido por observação direta. Isso nos previne de aceitar tão inocentemente como válido um “modelo confuso” para representar a realidade. Por ele mesmo ele não explicaria qualquer coisa imprecisa ou contraditória. Existe uma diferença entre uma fotografia tremida ou desfocada e uma foto de nuvens e neblina.”
Sobre o experimento, Schrödinger escreveu:
“Qualquer um pode mesmo montar casos bem ridículos. Um gato é preso em uma câmara de aço, enquanto com o dispositivo seguinte (o qual deve estar seguro contra interferência direta do gato): em um contador Geiger tem uma pequena quantidade de substância radioativa, tão pequena, que talvez durante o período de uma hora, um dos átomos decaia, mas também, com a mesma probabilidade, talvez nenhum; se isso acontecer, o tubo do contador descarrega e através de um relé libera um martelo que quebra um pequeno frasco de ácido cianídrico. Se algum deles tiver saído do seu sistema natural por uma hora, alguém pode concluir que o gato permanece vivo enquanto o átomo não tiver decaído. Afunção-psi do sistema poderia ser expresso por ter dentro dele o gato morto-vivo (com o perdão da palavra) misturada ou dividido em partes iguais.
É típico desses casos que uma indeterminação originalmente restrita ao domínio atômico tenha sido transformada em uma indeterminação macroscópica, o qual pode então ser resolvido por observação direta. Isso nos previne de aceitar tão inocentemente como válido um “modelo confuso” para representar a realidade. Por ele mesmo ele não explicaria qualquer coisa imprecisa ou contraditória. Existe uma diferença entre uma fotografia tremida ou desfocada e uma foto de nuvens e neblina.”
O texto acima é a tradução de dois parágrafos do artigo original bem mais extenso, o qual aparece na revista alemã Naturwissenschaften (“Ciências Naturais”) em 1935.
A famosa experiência mental de Schrödinger coloca a questão: quando o sistema quântico para de ser uma mistura de estados e se torna ou um ou o outro? (Mais tecnicamente, quando o atual estado quântico para de ser uma combinação linear de estados, cada um dos quais se parece com estados clássicos diferentes, e em vez disso começar a ter apenas uma clássica descrição?) Se o gato sobreviver, isso lembra que ele está apenas vivo. Mas as explicações das experiências EPR que são consistentes com a mecânica quântica microscópica padrão requer que objetos macroscópicos, como gatos e cadernos, não podem ter sempre apenas uma descrição clássica. O propósito da experiência mental é para ilustrar esse aparente paradoxo: nossa intuição diz que nenhum observador pode estar em uma mistura de estados, mesmo que eles sejam gatos, por exemplo, eles não podem estar em tal mistura. É necessário que os gatos sejam observadores, ou sua existência em um estado clássico simples e bem definido exige outro observador externo? Cada alternativa pareceu absurda para Albert Einstein, que estava impressionado pela habilidade do experimento mental para esclarecer esses problemas; em uma carta à Schrödinger datada de 1950 ele escreveu:
A famosa experiência mental de Schrödinger coloca a questão: quando o sistema quântico para de ser uma mistura de estados e se torna ou um ou o outro? (Mais tecnicamente, quando o atual estado quântico para de ser uma combinação linear de estados, cada um dos quais se parece com estados clássicos diferentes, e em vez disso começar a ter apenas uma clássica descrição?) Se o gato sobreviver, isso lembra que ele está apenas vivo. Mas as explicações das experiências EPR que são consistentes com a mecânica quântica microscópica padrão requer que objetos macroscópicos, como gatos e cadernos, não podem ter sempre apenas uma descrição clássica. O propósito da experiência mental é para ilustrar esse aparente paradoxo: nossa intuição diz que nenhum observador pode estar em uma mistura de estados, mesmo que eles sejam gatos, por exemplo, eles não podem estar em tal mistura. É necessário que os gatos sejam observadores, ou sua existência em um estado clássico simples e bem definido exige outro observador externo? Cada alternativa pareceu absurda para Albert Einstein, que estava impressionado pela habilidade do experimento mental para esclarecer esses problemas; em uma carta à Schrödinger datada de 1950 ele escreveu:
“Você é o único físico contemporâneo, além de Laue, que vê o que ninguém consegue sobre a assunção da realidade – se pelo menos alguém estiver sendo honesto. A maioria deles simplesmente não vê o tipo de jogo arriscado que eles estão jogando com a realidade – a realidade é algo independente do que já for a experimentalmente visto. A interpretação deles é, entretanto, refutada mais elegantemente pelo seu sistema de átomo radioativo + amplificador + carga de pólvora + gato em uma caixa, no qual a função-psi do sistema contém ambos gato vivo e explodido em pedaços. Ninguém realmente duvida que a presença ou ausência do gato é algo independente do ato de observação.”
Note que nenhuma carga de pólvora é mencionada no esquema de Schrödinger, que usa um contador Geiger como amplificador e cianeto no lugar de pólvora; a pólvora foi apenas mencionada na sugestão original de Einstein para Schrödinger 15 anos antes.
1. Paradoxo EPR


Na mecânica quântica, o paradoxo EPR ou Paradoxo de Einstein-Podolsky-Rosen é um experimento mental que demonstra que o resultado de uma medição realizada em uma parte do sistema quântico pode ter um efeito instantâneo no resultado de uma medição realizada em outra parte, independentemente da distância que separa as duas partes. Isto vai de encontro aos princípios da relatividade especial, que estabelece que a informação não pode ser transmitida mais rapidamente que a velocidade da luz. “EPR” vem das iniciais de Albert Einstein, Boris Podolsky, e Nathan Rosen, que apresentaram este experimento mental em um trabalho em 1935 que buscava demonstrar que a mecânica quântica não é uma teoria física completa. É algumas vezes denominado como paradoxo EPRB devido a David Bohm, que converteu o experimento mental inicial em algo próximo a um experimento viável.
O EPR é um paradoxo no seguinte sentido: se se tomar a mecânica quântica e a ela adicionar uma condição aparentemente razoável (tal como “localidade”, “realismo” ou “inteireza”), obtém-se umacontradição. Porém, a mecânica quântica por si só não apresenta nenhuma inconsistência interna, nem — como isto poderia sugerir — contradiz a teoria relativística. Como um resultado de desenvolvimentos teóricos e experimentais seguintes ao trabalho original da EPR, a maioria dos físicos atuais concorda que o paradoxo EPR é um exemplo de como a mecânica quântica viola o ponto de vista esperado na clássica, e não como uma indicação de que a mecânica quântica seja falha e sim inaplicável ao meio.inconsistência interna, nem — como isto poderia sugerir — contradiz a teoria relativística. Como um resultado de desenvolvimentos teóricos e experimentais seguintes ao trabalho original da EPR, a maioria dos físicos atuais concorda que o paradoxo EPR é um exemplo de como a mecânica quântica viola o ponto de vista esperado na clássica, e não como uma indicação de que a mecânica quântica seja falha e sim inaplicável ao meio.
O paradoxo EPR apóia-se em um fenômeno predito pela mecânica quântica e conhecido como entrelaçamento quântico, que mostra que medições realizadas em partes separadas de um sistema quântico influenciam-se mutuamente. Este efeito é atualmente conhecido como “comportamento não local” (ou, coloquialmente, como “estranheza quântica”). De forma a ilustrar isto, considere a seguinte versão simplificada do experimento mental EPR devido a Bohm.
Medições em um estado de entrelaçamento
Tem-se uma fonte emissora de pares de elétrons, com um elétron enviado para o destino A, onde existe uma observadora chamada Alice, e outro enviado para o destino B, onde existe um observador chamado Bob. De acordo com a mecânica quântica, podemos arranjar nossa fonte de forma tal que cada par de elétrons emitido ocupe um estado quântico conhecido como spin singlet. Isto pode ser visto como uma superposição quântica de dois estados; sejam eles I e II. No estado I, o elétron A tem spin apontado para cima ao longo do eixo z (+z) e o elétron B tem seu spin apontando para baixo ao longo do mesmo eixo (-z). No estado II, o elétron A tem spin -z e o elétron B, +z. Portanto, é impossível associar qualquer um dos elétrons em um spin singlet, com um estado definido de spin. Os elétrons estão, portanto, no chamado entrelaçamento.
Alice mede neste momento o spin no eixo z. Ela pode obter duas possíveis respostas: +z ou -z. Suponha que ela obteve +z. De acordo com a mecânica quântica, o estado quântico do sistemacolapsou para o estado I. (Diferentes interpretações da mecânica quântica têm diferentes formas de dizer isto, mas o resultado básico é o mesmo). O estado quântico determina a probabilidade das respostas de qualquer medição realizada no sistema. Neste caso, se Bob a seguir medir o spin no eixo z, ele obterá -z com 100% de certeza. Similarmente, se Alice obtiver -z, Bob terá +z.
Não há, certamente, nada de especial quanto à escolha do eixo z. Por exemplo, suponha que Alice e Bob agora decidam medir o spin no eixo x. De acordo com a mecânica quântica, o estado do spin singlet deve estar exprimido igualmente bem como uma superposição dos estados de spin orientados na direção x. Chamemos tais estados de Ia e IIa. No estado Ia, o elétron de Alice tem o spin+x e o de Bob, -x. No estado IIa, o elétron de Alice tem spin -x e o de Bob, +x. Portanto, se Alice mede +x, o sistema colapsa para Ia e Bob obterá -x. Por outro lado, se Alice medir -x, o sistema colapsa para IIa e Bob obterá +x.
Em mecânica quântica, o spin x e o spin z são “observáveis incompatíveis”, que significa que há um principio da incerteza de Heisenberg operando entre eles: um estado quântico não pode possuir um valor definido para ambas as variáveis. Suponha que Alice meça o spin z e obtenha +z, com o estado quântico colapsando para o estado I. Agora, ao invés de medir o spin z também, suponha que Bob meça o spin x. De acordo com a mecânica quântica, quando o sistema está no estado I, a medição do spin x de Bob terá uma probabilidade de 50% de produzir +x e 50% de -x. Além disso, é fundamentalmente impossível predizer qual resultado será obtido até o momento que Bob realize a medição.
Incidentalmente, embora tenhamos usado o spin como exemplo, muitos tipos de quantidades físicas — que a mecânica quântica denomina como “observáveis” — podem ser usados para produzir entrelaçamento quântico. O artigo original de EPR usou o momento como observável. Experimentos atuais abordando o contexto de EPR frequentemente usam a polarização de fótons, porque são experiências mais fáceis de se preparar e medir.
O EPR é um paradoxo no seguinte sentido: se se tomar a mecânica quântica e a ela adicionar uma condição aparentemente razoável (tal como “localidade”, “realismo” ou “inteireza”), obtém-se umacontradição. Porém, a mecânica quântica por si só não apresenta nenhuma inconsistência interna, nem — como isto poderia sugerir — contradiz a teoria relativística. Como um resultado de desenvolvimentos teóricos e experimentais seguintes ao trabalho original da EPR, a maioria dos físicos atuais concorda que o paradoxo EPR é um exemplo de como a mecânica quântica viola o ponto de vista esperado na clássica, e não como uma indicação de que a mecânica quântica seja falha e sim inaplicável ao meio.inconsistência interna, nem — como isto poderia sugerir — contradiz a teoria relativística. Como um resultado de desenvolvimentos teóricos e experimentais seguintes ao trabalho original da EPR, a maioria dos físicos atuais concorda que o paradoxo EPR é um exemplo de como a mecânica quântica viola o ponto de vista esperado na clássica, e não como uma indicação de que a mecânica quântica seja falha e sim inaplicável ao meio.
O paradoxo EPR apóia-se em um fenômeno predito pela mecânica quântica e conhecido como entrelaçamento quântico, que mostra que medições realizadas em partes separadas de um sistema quântico influenciam-se mutuamente. Este efeito é atualmente conhecido como “comportamento não local” (ou, coloquialmente, como “estranheza quântica”). De forma a ilustrar isto, considere a seguinte versão simplificada do experimento mental EPR devido a Bohm.
Medições em um estado de entrelaçamento
Tem-se uma fonte emissora de pares de elétrons, com um elétron enviado para o destino A, onde existe uma observadora chamada Alice, e outro enviado para o destino B, onde existe um observador chamado Bob. De acordo com a mecânica quântica, podemos arranjar nossa fonte de forma tal que cada par de elétrons emitido ocupe um estado quântico conhecido como spin singlet. Isto pode ser visto como uma superposição quântica de dois estados; sejam eles I e II. No estado I, o elétron A tem spin apontado para cima ao longo do eixo z (+z) e o elétron B tem seu spin apontando para baixo ao longo do mesmo eixo (-z). No estado II, o elétron A tem spin -z e o elétron B, +z. Portanto, é impossível associar qualquer um dos elétrons em um spin singlet, com um estado definido de spin. Os elétrons estão, portanto, no chamado entrelaçamento.
Alice mede neste momento o spin no eixo z. Ela pode obter duas possíveis respostas: +z ou -z. Suponha que ela obteve +z. De acordo com a mecânica quântica, o estado quântico do sistemacolapsou para o estado I. (Diferentes interpretações da mecânica quântica têm diferentes formas de dizer isto, mas o resultado básico é o mesmo). O estado quântico determina a probabilidade das respostas de qualquer medição realizada no sistema. Neste caso, se Bob a seguir medir o spin no eixo z, ele obterá -z com 100% de certeza. Similarmente, se Alice obtiver -z, Bob terá +z.
Não há, certamente, nada de especial quanto à escolha do eixo z. Por exemplo, suponha que Alice e Bob agora decidam medir o spin no eixo x. De acordo com a mecânica quântica, o estado do spin singlet deve estar exprimido igualmente bem como uma superposição dos estados de spin orientados na direção x. Chamemos tais estados de Ia e IIa. No estado Ia, o elétron de Alice tem o spin+x e o de Bob, -x. No estado IIa, o elétron de Alice tem spin -x e o de Bob, +x. Portanto, se Alice mede +x, o sistema colapsa para Ia e Bob obterá -x. Por outro lado, se Alice medir -x, o sistema colapsa para IIa e Bob obterá +x.
Em mecânica quântica, o spin x e o spin z são “observáveis incompatíveis”, que significa que há um principio da incerteza de Heisenberg operando entre eles: um estado quântico não pode possuir um valor definido para ambas as variáveis. Suponha que Alice meça o spin z e obtenha +z, com o estado quântico colapsando para o estado I. Agora, ao invés de medir o spin z também, suponha que Bob meça o spin x. De acordo com a mecânica quântica, quando o sistema está no estado I, a medição do spin x de Bob terá uma probabilidade de 50% de produzir +x e 50% de -x. Além disso, é fundamentalmente impossível predizer qual resultado será obtido até o momento que Bob realize a medição.
Incidentalmente, embora tenhamos usado o spin como exemplo, muitos tipos de quantidades físicas — que a mecânica quântica denomina como “observáveis” — podem ser usados para produzir entrelaçamento quântico. O artigo original de EPR usou o momento como observável. Experimentos atuais abordando o contexto de EPR frequentemente usam a polarização de fótons, porque são experiências mais fáceis de se preparar e medir.
Realidade e integridade
Introduziremos agora dois novos conceitos usados por Einstein, Podolsky, e Rosen, que são cruciais em seu ataque à mecânica quântica: (i) os elementos da realidade física e (ii) a integridade de uma teoria física.
Os autores não se referem diretamente ao significado filosófico de um “elemento da realidade física”. Ao invés disso, assumem que se o valor de qualquer quantidade física de um sistema pode ser predito com absoluta certeza antes de se realizar uma medição ou, em outras palavras, perturbando-o, então tal valor corresponde a um elemento da realidade física. Note que o oposto não é necessariamente verdadeiro; poderia haver outros caminhos para existir elementos da realidade física, mas isto não afeta o argumento.
A seguir, EPR definiu uma “teoria física completa” como aquela na qual cada elemento da realidade física tem relevância. O objetivo deste artigo era mostrar, usando estas duas definições, que a mecânica quântica não é uma teoria física completa.
Vejamos como estes conceitos se aplicam para o experimento mental acima. Suponha que Alice decida medir o valor do spin no eixo z (chamemo-no de spin z.) Depois de Alice realizar sua medição, o spin z do elétron de Bob é definitivamente conhecido, de forma que torna-se um elemento da realidade física. De modo similar, se Alice decide medir o spin no eixo x, o spin x do elétron de Bob torna-se um elemento da realidade física logo após a medição por Alice.
Vimos que um estado quântico não pode possuir um valor definido para ambos eixos, x e z. Se a mecânica quântica é uma teoria física completa no sentido dado acima, os spin x e z não podem ser elementos da mesma realidade ao mesmo tempo. Isto significa que a decisão de Alice — de escolher se faz a medição no eixo x ou z — tem um efeito instantâneo nos elementos da realidade física na localidade de Bob. Contudo, isto viola outro princípio, o da localidade.
Introduziremos agora dois novos conceitos usados por Einstein, Podolsky, e Rosen, que são cruciais em seu ataque à mecânica quântica: (i) os elementos da realidade física e (ii) a integridade de uma teoria física.
Os autores não se referem diretamente ao significado filosófico de um “elemento da realidade física”. Ao invés disso, assumem que se o valor de qualquer quantidade física de um sistema pode ser predito com absoluta certeza antes de se realizar uma medição ou, em outras palavras, perturbando-o, então tal valor corresponde a um elemento da realidade física. Note que o oposto não é necessariamente verdadeiro; poderia haver outros caminhos para existir elementos da realidade física, mas isto não afeta o argumento.
A seguir, EPR definiu uma “teoria física completa” como aquela na qual cada elemento da realidade física tem relevância. O objetivo deste artigo era mostrar, usando estas duas definições, que a mecânica quântica não é uma teoria física completa.
Vejamos como estes conceitos se aplicam para o experimento mental acima. Suponha que Alice decida medir o valor do spin no eixo z (chamemo-no de spin z.) Depois de Alice realizar sua medição, o spin z do elétron de Bob é definitivamente conhecido, de forma que torna-se um elemento da realidade física. De modo similar, se Alice decide medir o spin no eixo x, o spin x do elétron de Bob torna-se um elemento da realidade física logo após a medição por Alice.
Vimos que um estado quântico não pode possuir um valor definido para ambos eixos, x e z. Se a mecânica quântica é uma teoria física completa no sentido dado acima, os spin x e z não podem ser elementos da mesma realidade ao mesmo tempo. Isto significa que a decisão de Alice — de escolher se faz a medição no eixo x ou z — tem um efeito instantâneo nos elementos da realidade física na localidade de Bob. Contudo, isto viola outro princípio, o da localidade.
Localidade no experimento EPR
O princípio da localidade estabelece que processos físicos ocorrendo em um determinado lugar não devem ter um efeito imediato em elementos da realidade em outro local. À primeira vista, isto parece ser uma presunção aceitável, já que parece ser uma conseqüência da relatividade especial, que estabelece que a informação nunca pode ser transmitida mais rapidamente que a velocidade da luz sem violar o princípio da causalidade. É uma crença geral que qualquer teoria que viole o princípio da causalidade deve possuir uma inconsistência interna.
Ou seja, a mecânica quântica viola o princípio da localidade, mas não o princípio da causalidade. A causalidade é preservada porque não há forma de Alice transmitir mensagens (isto é, informação) a Bob pela interferência na escolha do eixo. Qualquer que seja o eixo que ela use, a probabilidade é de 50% de se obter “+” e 50% de se obter “-”, de forma completamente aleatória; de acordo com a mecânica quântica, é fundamentalmente impossível para ela influenciar o resultado que ela obterá. Além disso, Bob é somente capaz de realizar sua medição uma única vez: há uma propriedade fundamental da mecânica quântica, conhecida como o “teorema anticlonagem”, que torna impossível a Bob fazer um milhão de cópias do elétron por ele recebido, realizar uma medição de spin em cada elétron, e estudar a distribuição estatística dos resultados. Portanto, na única medição que lhe é permitido fazer, há uma probabilidade de 50% de obter “+” e 50% de “-”, independente se o eixo escolhido está alinhado de acordo com o de Alice.
Porém, o princípio da localidade apóia-se muito na intuição, e Einstein, Podolsky e Rosen não puderam abandoná-la. Einstein brincou, dizendo que as predições na mecânica quântica eram “estranhas ações a distância”. A conclusão que eles esboçaram era a de que a mecânica quântica não é uma teoria completa.
Deve-se notar que a palavra localidade tem vários significados na Física. Por exemplo, na teoria quântica de campo, “localidade” significa que os campos quânticos em diferentes pontos no espaço não interagem entre si. Porém, teorias de campo quântico que são “locais” neste sentido violam o princípio da localidade como definido por EPR.
O princípio da localidade estabelece que processos físicos ocorrendo em um determinado lugar não devem ter um efeito imediato em elementos da realidade em outro local. À primeira vista, isto parece ser uma presunção aceitável, já que parece ser uma conseqüência da relatividade especial, que estabelece que a informação nunca pode ser transmitida mais rapidamente que a velocidade da luz sem violar o princípio da causalidade. É uma crença geral que qualquer teoria que viole o princípio da causalidade deve possuir uma inconsistência interna.
Ou seja, a mecânica quântica viola o princípio da localidade, mas não o princípio da causalidade. A causalidade é preservada porque não há forma de Alice transmitir mensagens (isto é, informação) a Bob pela interferência na escolha do eixo. Qualquer que seja o eixo que ela use, a probabilidade é de 50% de se obter “+” e 50% de se obter “-”, de forma completamente aleatória; de acordo com a mecânica quântica, é fundamentalmente impossível para ela influenciar o resultado que ela obterá. Além disso, Bob é somente capaz de realizar sua medição uma única vez: há uma propriedade fundamental da mecânica quântica, conhecida como o “teorema anticlonagem”, que torna impossível a Bob fazer um milhão de cópias do elétron por ele recebido, realizar uma medição de spin em cada elétron, e estudar a distribuição estatística dos resultados. Portanto, na única medição que lhe é permitido fazer, há uma probabilidade de 50% de obter “+” e 50% de “-”, independente se o eixo escolhido está alinhado de acordo com o de Alice.
Porém, o princípio da localidade apóia-se muito na intuição, e Einstein, Podolsky e Rosen não puderam abandoná-la. Einstein brincou, dizendo que as predições na mecânica quântica eram “estranhas ações a distância”. A conclusão que eles esboçaram era a de que a mecânica quântica não é uma teoria completa.
Deve-se notar que a palavra localidade tem vários significados na Física. Por exemplo, na teoria quântica de campo, “localidade” significa que os campos quânticos em diferentes pontos no espaço não interagem entre si. Porém, teorias de campo quântico que são “locais” neste sentido violam o princípio da localidade como definido por EPR.
Resolvendo o paradoxo
Variáveis ocultas
Há vários possíveis caminhos para se resolver o paradoxo EPR. Um deles, sugerido por EPR, é que a mecânica quântica, a despeito do seu sucesso em uma ampla variedade de contextos experimentais, é ainda uma teoria incompleta. Em outras palavras, há ainda uma teoria natural a ser desvendada, à qual a mecânica quântica age no papel de uma aproximação estatística (uma excelente aproximação, sem dúvida). Diferente da mecânica quântica, esta teoria mais completa conteria variáveis correspondentes a todos os “elementos da realidade”. Deve haver algum mecanismo desconhecido atuando nestas variáveis de modo a ocasionar os efeitos observados de “não-comutação dos observáveis quânticos”, isto é, o princípio da incerteza de Heisenberg. Tal teoria é conhecida como teoria das variáveis ocultas.
Para ilustrar esta idéia, podemos formular uma teoria de variável oculta bem simples para o experimento mental anterior. Supõe-se que o estado do spin singlet emitido pela fonte é na verdade uma descrição aproximada do “verdadeiro” estado físico, com valores definidos para o spin z e o spin x. Neste estado “verdadeiro”, o elétron que vai para Bob sempre tem valor de spin oposto ao do elétron que vai para Alice, mas, por outro lado, os valores são completamente aleatórios. Por exemplo, o primeiro par emitido pela fonte poderia ser “(+z, -x) para Alice e (-z, +x) para Bob”, o próximo par “(-z, -x) para Alice e (+z, +x) para Bob”, e assim por diante. Dessa forma, se o eixo de medição de Bob estiver alinhado com o de Alice, ele necessariamente obterá sempre o oposto daquilo que Alice obtiver; por outro lado, ele terá “+” e “-” com a mesma probabilidade.
Assumindo que restrinjamo-nos a medir nos eixos z e x, a teoria de variáveis ocultas é experimentalmente indistinguível da mecânica quântica. Na realidade, certamente, há um (incontável) número de eixos nos quais Alice e Bob podem realizar suas medições, de forma que haverá infinito número de variáveis ocultas independentes! Contudo, isto não é um problema sério; apenas formulamos uma teoria de variáveis ocultas muito simplista; uma teoria mais sofisticada poderia “consertá-la”. Ou seja, ainda há um grande desafio por vir à idéia de variáveis ocultas.
Para ilustrar esta idéia, podemos formular uma teoria de variável oculta bem simples para o experimento mental anterior. Supõe-se que o estado do spin singlet emitido pela fonte é na verdade uma descrição aproximada do “verdadeiro” estado físico, com valores definidos para o spin z e o spin x. Neste estado “verdadeiro”, o elétron que vai para Bob sempre tem valor de spin oposto ao do elétron que vai para Alice, mas, por outro lado, os valores são completamente aleatórios. Por exemplo, o primeiro par emitido pela fonte poderia ser “(+z, -x) para Alice e (-z, +x) para Bob”, o próximo par “(-z, -x) para Alice e (+z, +x) para Bob”, e assim por diante. Dessa forma, se o eixo de medição de Bob estiver alinhado com o de Alice, ele necessariamente obterá sempre o oposto daquilo que Alice obtiver; por outro lado, ele terá “+” e “-” com a mesma probabilidade.
Assumindo que restrinjamo-nos a medir nos eixos z e x, a teoria de variáveis ocultas é experimentalmente indistinguível da mecânica quântica. Na realidade, certamente, há um (incontável) número de eixos nos quais Alice e Bob podem realizar suas medições, de forma que haverá infinito número de variáveis ocultas independentes! Contudo, isto não é um problema sério; apenas formulamos uma teoria de variáveis ocultas muito simplista; uma teoria mais sofisticada poderia “consertá-la”. Ou seja, ainda há um grande desafio por vir à idéia de variáveis ocultas.
Desigualdade de Bell
Em 1964, John Bell mostrou que as predições da mecânica quântica no experimento mental de EPR são sempre ligeiramente diferentes das predições de uma grande parte das teorias de variáveis ocultas. Grosseiramente falando, a mecânica quântica prediz uma correlação estatística ligeiramente mais forte entre os resultados obtidos em diferentes eixos do que o obtido pelas teorias de variáveis ocultas. Estas diferenças, expressas através de relações de desigualdades conhecidas como “desigualdades de Bell”, são em princípio detectáveis experimentalmente. Para uma análise mais detalhada deste estudo, veja teorema de Bell.
Depois da publicação do trabalho de Bell, inúmeros experimentos foram idealizados para testar as desigualdades de Bell. (Como mencionado acima, estes experimentos geralmente baseiam-se na medição da polarização de fótons). Todos os experimentos feitos até hoje encontraram comportamento similar às predições obtidas da mecânica quântica padrão.
Porém, este campo ainda não está completamente definido. Antes de mais nada, o teorema de Bell não se aplica a todas as possíveis teorias “realistas”. É possível construir uma teoria que escape de suas implicações e que são, portanto, indistinguíveis da mecânica quântica; porém, estas teorias são geralmente não-locais — parecem violar a casualidade e as regras da relatividade especial. Alguns estudiosos neste campo têm tentado formular teorias de variáveis ocultas que exploram brechas nos experimentos atuais, tais como brechas nas hipóteses feitas para a interpretação dos dados experimentais. Todavia, ninguém ainda conseguiu formular uma teoria realista localmente que possa reproduzir todos os resultados da mecânica quântica.
Depois da publicação do trabalho de Bell, inúmeros experimentos foram idealizados para testar as desigualdades de Bell. (Como mencionado acima, estes experimentos geralmente baseiam-se na medição da polarização de fótons). Todos os experimentos feitos até hoje encontraram comportamento similar às predições obtidas da mecânica quântica padrão.
Porém, este campo ainda não está completamente definido. Antes de mais nada, o teorema de Bell não se aplica a todas as possíveis teorias “realistas”. É possível construir uma teoria que escape de suas implicações e que são, portanto, indistinguíveis da mecânica quântica; porém, estas teorias são geralmente não-locais — parecem violar a casualidade e as regras da relatividade especial. Alguns estudiosos neste campo têm tentado formular teorias de variáveis ocultas que exploram brechas nos experimentos atuais, tais como brechas nas hipóteses feitas para a interpretação dos dados experimentais. Todavia, ninguém ainda conseguiu formular uma teoria realista localmente que possa reproduzir todos os resultados da mecânica quântica.
Implicações para a mecânica quântica
A maioria dos físicos atualmente acredita que a mecânica quântica é correta, e que o paradoxo EPR é somente um “paradoxo” porque a intuição clássica não corresponde à realidade física. Várias conclusões diferentes podem ser esboçadas a partir desta, dependendo de qual interpretação de mecânica quântica se use. Na velha interpretação de Copenhague, conclui-se que o principio da localidade não se aplica e que realmente ocorrem colapsos da função de onda. Na interpretação de muitos mundos, a localidade é preservada, e os efeitos da medição surgem da separação dos observadores em diferentes “históricos”.
O paradoxo EPR aprofundou a nossa compreensão da mecânica quântica pela exposição de características não-clássicas do processo de medição. Antes da publicação do paradoxo EPR, uma medição era freqüentemente visualizada como uma perturbação física que afetava diretamente o sistema sob medição. Por exemplo, quando se media a posição de um elétron, imaginava-se o disparo de uma luz nele, que afetava o elétron e que produzia incertezas quanto a sua posição. Tais explicações, que ainda são encontradas em explicações populares de mecânica quântica, foram revisadas pelo paradoxo EPR, o qual mostra que uma “medição” pode ser realizada em uma partícula sem perturbá-la diretamente, pela realização da medição em uma partícula entrelaçada distante.
Tecnologias baseadas no entrelaçamento quântico estão atualmente em desenvolvimento. Na criptografia quântica, partículas entrelaçadas são usadas para transmitir sinais que não podem servazados sem deixar traços. Na computação quântica, partículas entrelaçadas são usadas para realizar cálculos em paralelo em computadores, o que permite que certos cálculos sejam realizados mais rapidamente do que um computador clássico jamais poderia fazer.
O paradoxo EPR aprofundou a nossa compreensão da mecânica quântica pela exposição de características não-clássicas do processo de medição. Antes da publicação do paradoxo EPR, uma medição era freqüentemente visualizada como uma perturbação física que afetava diretamente o sistema sob medição. Por exemplo, quando se media a posição de um elétron, imaginava-se o disparo de uma luz nele, que afetava o elétron e que produzia incertezas quanto a sua posição. Tais explicações, que ainda são encontradas em explicações populares de mecânica quântica, foram revisadas pelo paradoxo EPR, o qual mostra que uma “medição” pode ser realizada em uma partícula sem perturbá-la diretamente, pela realização da medição em uma partícula entrelaçada distante.
Tecnologias baseadas no entrelaçamento quântico estão atualmente em desenvolvimento. Na criptografia quântica, partículas entrelaçadas são usadas para transmitir sinais que não podem servazados sem deixar traços. Na computação quântica, partículas entrelaçadas são usadas para realizar cálculos em paralelo em computadores, o que permite que certos cálculos sejam realizados mais rapidamente do que um computador clássico jamais poderia fazer.
BÔNUS- Suicídio Quantico
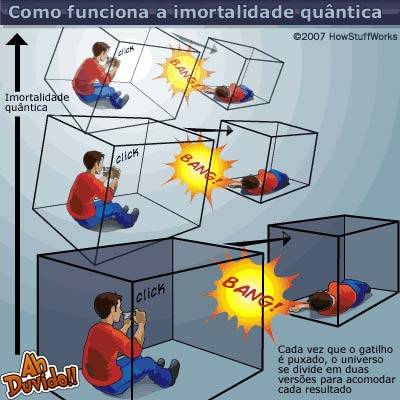

Um homem se senta em frente a uma arma, apontada para sua cabeça. Não é uma arma comum; ela está ligada a uma máquina que mede o giro de uma partícula quântica. Cada vez que o gatilho é puxado, o giro da partícula quântica – ou quark – é medido. Dependendo da medida, a arma dispara ou não. Se a medida mostrar que a partícula quântica está girando no sentido horário, a arma dispara. Se o quark estiver girando no sentido anti-horário, a arma não dispara. O gatilho só faz um clique.
Nervoso, o homem respira fundo e puxa o gatilho. O gatilho só faz clique. Ele puxa o gatilho de novo. Clique. De novo: clique. O homem vai continuar puxando o gatilho de novo, de novo, com o mesmo resultado: a arma não vai disparar. Apesar de estar funcionando corretamente e carregada, não importa quantas vezes ele puxe o gatilho, a arma nunca vai disparar. Ele vai continuar o processo eternamente, tornando-se imortal (em inglês).
Volte no tempo até o início do experimento. O homem puxa o gatilho pela primeira vez, e a medida mostra que o quark está girando no sentido horário. A arma dispara. O homem morre.
Mas calma lá. O homem já puxou o gatilho a primeira vez – e infinitas vezes depois disso – e já sabemos que a arma não disparou. Como o homem pode estar morto? Ele não sabe disso, mas está vivo e morto. Cada vez que ele puxa o gatilho, o universo se divide em dois. E vai continuar a se dividir cada vez que o gatilho é puxado [fonte: Tegmark (em inglês)].
Este experimento mental é chamado de suicídio quântico. Foi introduzido pelo então teórico da Universidade de Princeton (em inglês) Max Tegmark em 1997 (atualmente professor do MIT – Instituto Tecnológico de Massachusetts).
Nervoso, o homem respira fundo e puxa o gatilho. O gatilho só faz clique. Ele puxa o gatilho de novo. Clique. De novo: clique. O homem vai continuar puxando o gatilho de novo, de novo, com o mesmo resultado: a arma não vai disparar. Apesar de estar funcionando corretamente e carregada, não importa quantas vezes ele puxe o gatilho, a arma nunca vai disparar. Ele vai continuar o processo eternamente, tornando-se imortal (em inglês).
Volte no tempo até o início do experimento. O homem puxa o gatilho pela primeira vez, e a medida mostra que o quark está girando no sentido horário. A arma dispara. O homem morre.
Mas calma lá. O homem já puxou o gatilho a primeira vez – e infinitas vezes depois disso – e já sabemos que a arma não disparou. Como o homem pode estar morto? Ele não sabe disso, mas está vivo e morto. Cada vez que ele puxa o gatilho, o universo se divide em dois. E vai continuar a se dividir cada vez que o gatilho é puxado [fonte: Tegmark (em inglês)].
Este experimento mental é chamado de suicídio quântico. Foi introduzido pelo então teórico da Universidade de Princeton (em inglês) Max Tegmark em 1997 (atualmente professor do MIT – Instituto Tecnológico de Massachusetts).

 .
.
 Ditador
Ditador
 Acesso
Acesso

 .
.
 QUE LEIO
QUE LEIO ESTRADA ATÉ AQUI...
ESTRADA ATÉ AQUI...




Nenhum comentário:
Postar um comentário